* 이진 탐색 트리 (Binary Search Tree)
"탐색을 위한 자료구조로 이진 트리를 사용하기 위해서 저장할 데이터의 크기에 따라 노드의 위치를 정의한 것"
- 전화번호부에서 전화번호를 찾거나
- 서점에서 책을 찾거나
- 지도에서 목적지를 찾는것
등과 같이 자료들 속에서 필요한 자료를 찾아내는 것이 탐색이다.
탐색을 하기 위해서 찾을 자료를 식별할 수 있는 유일한 값이 필요한데 이것을 키(key)라고 한다.
사람을 찾을 때 그 사람을 식별할 수 있는 주민등록번호나 학번을 사용하였다면 이것이 탐색키가 된다.
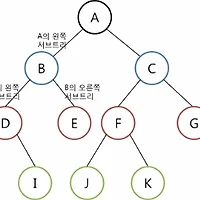
효율적인 탐색 작업을 위해 이진 탐색 트리를 다음과 같이 정의한다.
(1) 모든 원소는 서로 다른 유일한 키를 갖는다.
(2) 왼쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 작다.
(3) 오른쪽 서브 트리에 있는 원소의 키는 그 루트의 키보다 크다.
(4) 왼쪽 서브 트리와 오른쪽 서브 트리도 이진탐색 트리다.
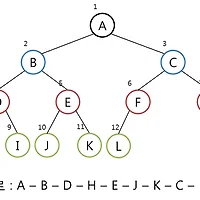
[ 이진 탐색 트리 탐색 연산 ]
탐색은 항상 루트 노드에서 시작한다.
먼저, 키값 x와 루트 노드의 키값을 비교한다.
if (x == 루트) 원하는 원소를 찾았으므로 탐색 성공
else if (루트 > x) 루트의 왼쪽 서브트리에 대해서 탐색 연산 수행
else if (루트 < x) 루트의 오른쪽 서브트리에 대해서 탐색 연산 수행
[ 이진 탐색 트리 삽입 연산 ]
원소를 삽입하려면 먼저 이진 탐색 트리에 같은 원소가 있는지를 확인하기 위해 탐색을 해야한다.
if (탐색 성공) 이미 같은 원소가 트리 내에 있는 것이므로 삽입 연산을 수행하지 않는다.
else if (탐색 실패) 크기를 비교하여 찾아간 노드의 위치에 같은 원소가 없는 것이므로 그 자리에 원소를 삽입
[ 이진 탐색 트리 삭제 연산 ]
원소를 삭제하는 경우 자식 노드의 수에 따라 세 가지 경우가 있다.
노드를 삭제한 후에도 여전히 이진 탐색트리를 유지해야 하기 때문에 각각의 경우에 따라 후속 처리가 필요하다.
① 삭제할 노드가 단말 노드인 경우
노드를 삭제하고, 부모노드의 링크 필드를 null로 설정하는 작업으로 간단히 처리할 수 있다.
② 삭제할 노드가 한 개의 자식노드를 가진 경우 (차수가 1인 경우)
노드를 삭제하고 나면 자식 노드가 트리에서 떨어져서 고아가 되어버린다.
남겨진 자식노드를 삭제한 부모노드의 자리로 올려준다.
자식이 부모의 유산을 물려받듯이 자식노드가 부모노드의 자리를 물려받는다.
③ 삭제할 노드가 두 개의 자식노드를 가진 경우 (차수가 2인 경우)
노드를 삭제하고 나면 부모노드의 자리를 자식노드에게 물려줄 때 왼쪽, 오른쪽 중 어느쪽에 물려줄 지 생각해야한다.
이진탐색 트리의 특성에 따라서 삭제할 노드의 자리에 위치할 값은 왼쪽 서브 트리에 있는 노드들의 값보다 커야하고, 오른쪽 서브 트리에 있는 노드들의 키값보다는 작아야한다.
그러므로 조상노드의 왼쪽 서브 트리에서 가장 큰 자손 노드 또는 오른쪽 서브 트리에서 가장 작은 자손 노드가 삭제할 노드의 자리에 올 수 있다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | package BST; public class TreeNode { char data; TreeNode left; TreeNode right; public TreeNode(){ this.left = null; this.right = null; } public TreeNode(char data){ this.data = data; this.left = null; this.right = null; } public Object getData(){ return data; } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | package BST; public class BinarySearchTree { private TreeNode root = new TreeNode(); public TreeNode insertKey(TreeNode root, char x) { TreeNode p = root; TreeNode newNode = new TreeNode(x); if(p==null){ return newNode; }else if(p.data>newNode.data){ p.left = insertKey(p.left, x); return p; }else if(p.data<newNode.data){ p.right = insertKey(p.right, x); return p; }else{ return p; } } public void insertBST(char x){ root = insertKey(root, x); } public TreeNode searchBST(char x){ TreeNode p = root; while(p!=null){ if(x<p.data) p = p.left; else if(x>p.data) p = p.right; else return p; } return p; } public void inorder(TreeNode root){ if(root!=null){ inorder(root.left); System.out.print(root.data + " "); inorder(root.right); } } public void printBST(){ inorder(root); System.out.println(); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | package BST; public class Test { public static void main(String[] args) { BinarySearchTree bst = new BinarySearchTree(); bst.insertBST('G'); bst.insertBST('I'); bst.insertBST('H'); bst.insertBST('D'); bst.insertBST('B'); bst.insertBST('M'); bst.insertBST('N'); bst.insertBST('A'); bst.insertBST('J'); bst.insertBST('E'); bst.insertBST('Q'); System.out.println("Binary Tree >>>"); bst.printBST(); System.out.println("Is There \"A\" ? >>> "); TreeNode p1 = bst.searchBST('A'); if(p1!=null){ System.out.println(p1.data + " 탐색 성공"); }else{ System.out.println("탐색 실패"); } System.out.println("Is There \"Z\" ? >>> "); TreeNode p2 = bst.searchBST('Z'); if(p2!=null){ System.out.println(p2.data + " 탐색 성공"); }else{ System.out.println("탐색 실패"); } } } |
'전산 기초 > 자료구조' 카테고리의 다른 글
| [자료구조/java] 힙 (Heap) - 배열 구현 (1) | 2015.11.11 |
|---|---|
| [자료구조/java] 이진 트리 (Binary Tree) 의 순회 (traversal) (5) | 2015.11.05 |
| [자료구조/java] 이진 트리 (Binary Tree) - 순차 자료구조 방식, 연결 자료구조 방식 (0) | 2015.11.05 |
| [자료구조/java] 이진 트리 (Binary Tree) (0) | 2015.11.05 |
| [자료구조/java] 트리 (Tree) (0) | 2015.11.05 |